Advances in screening and identification in math MTSS
By Dr. Amanda VanDerHeyden, SpringMath author, policy advisor, thought leader, and researcher
Curriculum-based measurement (CBM) was game changing in education because it created standardized, reliable, and valid scores that could be used to evaluate and adjust instruction for better learning (Stecker, et al, 2005). But CBM in math differs from CBM in reading.
Researchers attempted to construct general outcome measures in math using a curricular sampling approach, meaning that researchers identified 3-5 skills that are reflective of the most important mathematical learning that is expected to occur during a school year. Those problems are then provided on a single probe. The rationale for curricular sampling is that as instruction progresses (and learning occurs), gains will be observed in a linear fashion as children master skills included on the measure. But the technical characteristics of these measures have always been weaker than those reported for reading CBM (Foegen et al., 2007; Nelson et al., 2023) and an “oral reading fluency” equivalent in math has never been found.
The problem of sensitivity and mastery measurement as an alternative
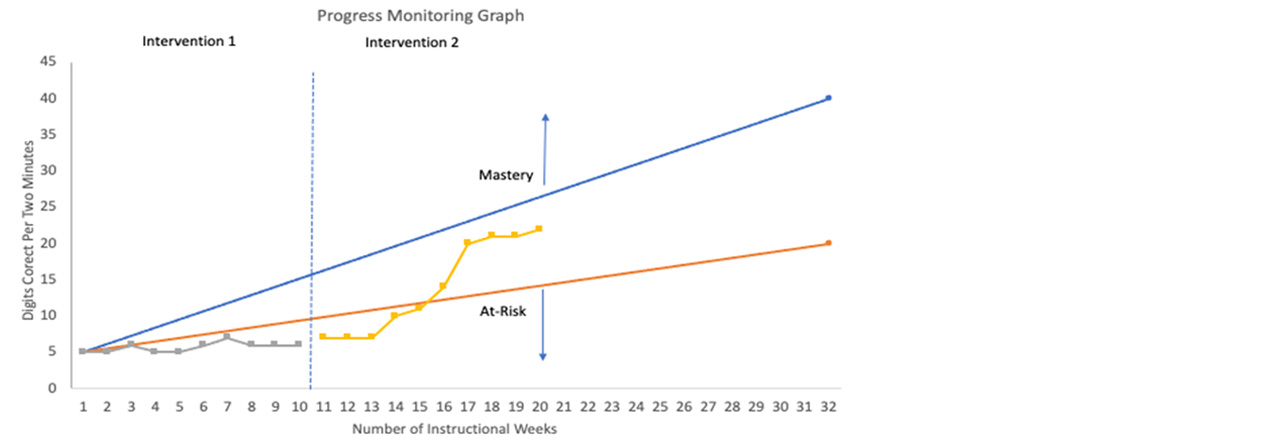
Two problems have become apparent with regard to multiple-skill measures intended to function as general outcome measures in math, and both are problems of sensitivity. CBMs are used during screening to identify students who may be at risk for poor learning outcomes and in need of intervention. With multiple-skill math measures, only a small number of problem types (i.e., no more than 4-5) can be used on a single measure, so the measures are constructed choosing 4-5 operational skills that are important for children to master during the school year. Therefore, children are assessed on problem types that they have not yet been taught how to do, especially at the beginning of the monitoring period. Thus, at the beginning of the monitoring period, score ranges will be severely constrained. These constrained scores destroy the capacity to use the scores to make screening decisions, which is especially important during the first half of the monitoring period when supplemental intervention could most usefully be added to prevent or repair detected gaps.
Similarly, in terms of progress monitoring, because the measure is intended to model growth during the course of the year, the gains between each assessment occasion will be so minimal that characterizing the success of instructional changes relative to “typical” growth becomes technically very difficult if not impossible. In concrete terms, a student in intervention might successfully improve the ability to multiply single digit whole numbers and identify common factors, but a mixed-skill measure that includes mostly fraction operations is unlikely to detect these gains and therefore is not useful as a basis for adjusting the intervention or interpreting its effects.
Figure 1. In this example, a general outcome measure is used to model growth or response to intervention. Too much time is required to determine whether the intervention has worked. General outcome measures in math are not sufficiently sensitive for progress monitoring in MTSS.
Mastery measurement, Goldilocks, and SpringMath
Given the limitations of sensitivity with math CBM, researchers began to study direct measurement of more specifically defined skills that were being taught in a known sequence (VanDerHeyden & Burns, 2008; VanDerHeyden & Burns, 2009; VanDerHeyden et al., 2017). Sampling a single skill allowed researchers to measure skill mastery with greater precision and permit more fine-tuned decision making about progress even if it changed the way progress was measured. In other words, if the right skills could be measured at the right moments of instruction, these data might be meaningful to formative assessment decisions. Such measures would have to change more frequently resulting in a series of shorter-term linear trends. Summative metrics like rate of skill mastery could function as key decision metrics. We think of mastery measurement in math as a series of “Goldilocks” measures (i.e., the right measure at the right time) closely connected to grade-level learning in mathematics. In other words, the key is that a well-constructed technically equivalent measure of a skill is used when that skill is being taught to model learning from acquisition to mastery.
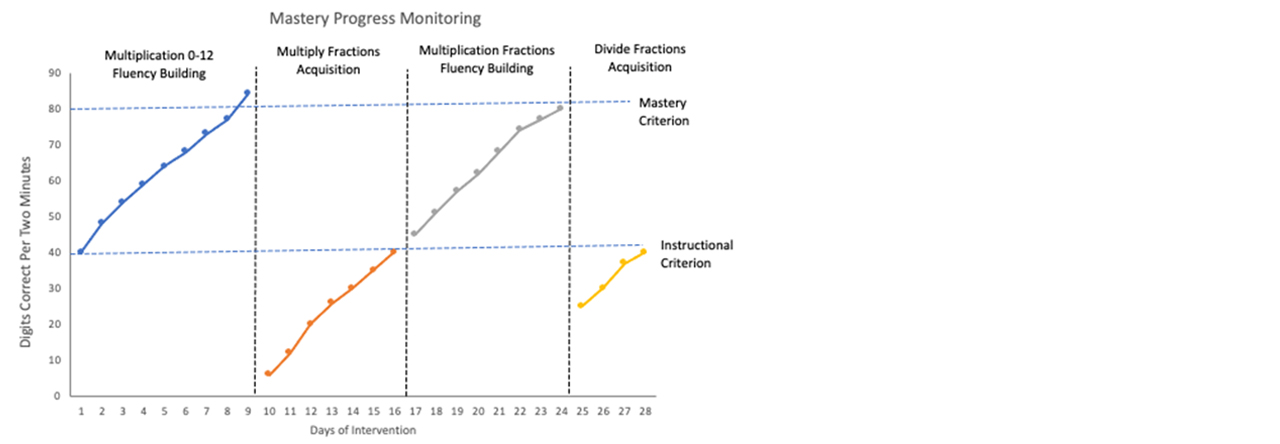
In the example below, a typical flow is shown for skills and instructional tactic. In the sample case here, a student begins intervention for fluency-building for multiplication facts 0-12. After reaching mastery, the intervention shifts to establish a new skill, which is multiplying with fractions. After reaching the instructional range, the intervention shifts to building fluency for multiplying with fractions. After reaching mastery for multiplying with fractions, the intervention shifts yet again to establish division of fractions. These instructional adjustments can be made much more quickly than would be possible with the use of less sensitive measures (e.g., multiple skill measures as shown in the last figure). Rapid intervention adjustment allows teachers to optimize intervention intensity for the student. Multiple-skill measures should also reflect gains, but with less steep gains.
Figure 2. Mastery measures reflect growth during intervention much more quickly and facilitate more rapid adjustment of the intervention to promote student learning. SpringMath uses mastery measurement to monitor and adjust the intervention.
A series of recent studies have demonstrated that mastery measurement in math met conventional standards of technical adequacy, including reliability (VanDerHeyden et al., 2020; Solomon et al., 2022) and classification accuracy (VanDerHeyden et al., 2017; VanDerHeyden et al., 2019). Mastery Measurement also provides a closer connection to instruction, permitting more sensitive feedback to the teacher about the instructional effects and allowing the teacher to make more rapid and fine-tuned adjustments to instruction to improve learning. For example, Burns et al. (2006) used mastery measurement in mathematics to predict skill retention and more rapid learning of more complex associated skills. This study suggested a method and a set of decision rules to determine skill mastery during instruction. In other words, teachers could assess students in the class using a 2-minute classwide measure and know whether students required additional acquisition instruction, fluency-building opportunities, or advancement to more challenging content. Subsequently, such measures have been used to specify optimal dosages of instruction (Codding et al., 2016; Duhon et al., 2020) and rates of improvement have been empirically examined in large-scale reviews to characterize the dimensions of intervention conditions that can affect rates of improvement on mastery measures (e.g., dosage of intervention, skill targeted) (Solomon et al., 2020). Mastery measures also yield datasets that can be used to determine classwide and individual student risk (i.e., screening) and to evaluate programs of instruction more generally.
The most exciting news from emerging measurement research in mathematics is the possibility of using technically strong (reliable, generalizable) measurements in highly efficient ways to drive instructional changes in the classroom the next day. In contrast with norm-referenced rules that simply tell decision makers how students perform relative to other students; mastery measurement data can be used to tell us how likely a student is to thrive given specific instructional tactics. Knowing that a student performs below the 20th percentile tells us nothing about which instructional tactics are likely to benefit that student and whether the student is likely to respond to intervention when given optimal instruction. But knowing that a student performs at a level that predicts the student will remember what has been taught, will experience more robust and more efficient learning of more complex associated content, and can adapt the skill or use the skill under different task demands is highly useful to instruction. From the teacher’s perspective, knowing that the student is lower performing than other students means nothing if the assessment does not help the teacher solve the problem. Mastery measurement in math is necessary for teachers to know whether instruction is working for students and what instruction is needed by their students. SpringMath uses mastery measurement to drive all decisions.
The first step in MTSS is screening. Screening measures need to be highly efficient because they need to be administered to all students. (SpringMath screenings can be viewed here.) SpringMath involves a layering of rules that are applied to identify and provide the level of intensity needed by students to advance learning for the individual student and more broadly for systems. The process begins with screening. Unlike many systems of assessment, SpringMath emphasizes functional benchmark criteria for decision making. In other words, specific answers correct per minute criteria are attached to each skill at each grade level to reflect frustrational, instructional, and mastery level performances. Frustrational performance is performance associated with higher error rates and poor skill retention. Instructional performance is performance reflecting a high probability of learning gains given high-quality skill practice. Mastery level performance is performance that is likely to be retained over time, associated with faster learning of related more complex skills, and flexible, generalized skill use including solving novel problem types.
The decision rule targets were initially based upon the best research in academic assessment including the criteria set forth by Deno and Mirkin (1977) which were taken directly from the field of Precision Teaching. These criteria were empirically evaluated and validated by Burns, et al. (2006), VanDerHeyden & Burns (2008), and VanDerHeyden & Burns (2009).
Prior screening research has found that classwide math intervention improves screening accuracy and is a necessary mechanism in screening models. MTSS decision models using the criteria built into SpringMath generate decisions that are more accurate, efficient, and equitable than teacher nomination and static screening alone (VanDerHeyden et al., 2003; VanDerHeyden & Witt, 2005; VanDerHeyden et al., 2007). Teachers and other data-interpretation leaders often believe that the consequence of not using classwide intervention is simply a loss of efficiency with too many students being recommended for individual intervention. But, in fact, the wrong children are recommended for individual intervention including both false-positive (children who did not really need individual intervention) and false-negative errors (missing children who really did need individual intervention) when classwide intervention is not used as part of the screening decision.
We recommend that schools include all students in SpringMath screening and classwide intervention when classwide intervention is recommended. Screening and classwide intervention data are used to show gains during intervention in the teacher and coach “Growth” tabs. These data are also used to provide powerful program evaluation data at the school level to see the effects of your MTSS math effort and to understand your implementation soft spots that can be improved for better math learning.
Additional recommended reading and resources:
References
Burns, M. K., VanDerHeyden, A. M., & Jiban, C. (2006). Assessing the instructional level for mathematics: A comparison of methods. School Psychology Review, 35, 401-418.
Codding, R., VanDerHeyden, Martin, R. J., & Perrault, L. (2016). Manipulating treatment dose: Evaluating the frequency of a small group intervention targeting whole number operations. Learning Disabilities Research & Practice, 31, 208- 220. https://doi.org/10.1111/ldrp.12120
Deno, S. L., & Mirkin, P. K. (1977). Data-based program modification: A manual. Reston, VA: Council for Exception Children.
Duhon, G. J., Poncy, B. C., Krawiec, C. F., Davis, R. E., Ellis-Hervey, N., & Skinner, C. H. (2020) Toward a more comprehensive evaluation of interventions: A dose-response curve analysis of an explicit timing intervention. School Psychology Review. https://doi.org/10.1080/2372966X.2020.1789435
Foegen, A., Jiban, C., & Deno, S. (2007). Progress monitoring in mathematics: A review of the literature. The Journal of Special Education, 41(2), 121–139.
Nelson, G., Kiss, A. J., Codding, R. S., McKevett, N. M., Schmitt, J. F., Park, S., Romero, M. E., Hwang, J. (2023). Review of curriculum-based measurement in mathematics: An update and extension of the literature, Journal of School Psychology, 97, 1-42, https://doi.org/10.1016/j.jsp.2022.12.001
Solomon, B. G., Poncy, B. C., Battista, C., & Campaña, K. V. (2020). A review of common rates of improvement when implementing whole-number math interventions. School Psychology, 35, 353-362.
Solomon, B., G., VanDerHeyden, A. M., Solomon, E. C., Korzeniewski, E. R., Payne, L. L., Campaña, K. V., & Dillon, C. R. (2022). Mastery Measurement in Mathematics and the Goldilocks Effect. School Psychology.
VanDerHeyden, A. M., & Burns, M. K. (2008). Examination of the utility of various measures of mathematics proficiency. Assessment for Effective Intervention, 33, 215-224. https://doi.org/10.1177/1534508407313482
VanDerHeyden, A. M., & Burns, M. K. (2009). Performance indicators in math: Implications for brief experimental analysis of academic performance. Journal of Behavioral Education, 18, 71-91. https://doi.org/10.1007/s10864-009-9081-x
VanDerHeyden, A. M., Broussard, C., & Burns, M. K. (2019). Classification agreement for gated screening in mathematics: Subskill mastery measurement and classwide intervention. Assessment for Effective Intervention. https://doi.org/10.1177/1534508419882484
VanDerHeyden, A. M., Codding, R., Martin, R. (2017). Relative value of common screening measures in mathematics. School Psychology Review, 46, 65-87. https://doi.org/10.1080/02796015.2017.12087608
VanDerHeyden, A. M. & Witt, J. C. (2005). Quantifying the context of assessment: Capturing the effect of base rates on teacher referral and a problem-solving model of identification. School Psychology Review, 34, 161-183.
VanDerHeyden, A. M., Witt, J. C., & Gilbertson, D. A (2007). Multi-Year Evaluation of the Effects of a Response to Intervention (RTI) Model on Identification of Children for Special Education. Journal of School Psychology, 45, 225-256. https://doi.org/10.1016/j.jsp.2006.11.004
VanDerHeyden, A. M., Witt, J. C., & Naquin, G. (2003). Development and validation of a process for screening referrals to special education. School Psychology Review, 32, 204-227.