Fluency before function: a case against early calculator use
By SpringMath author Dr. Amanda VanDerHeyden
Recently my son was home on his college break and studying for the Medical College Admission Test (commonly called the MCAT). He mentioned to me that calculators are not allowed on the MCAT. So after he took a full-length, timed practice exam, I asked if I could have his scratch paper. As you might imagine, most of the math required involves converting quantities to solve problems in a content area like chemistry.
On his scratch paper, I saw long division, conversion of negative exponents, operations with fractions, and multidigit multiplication. These might seem like simple skills, but that is exactly how math works. There are about 145 high-leverage computation skills, the mastery of which opens the door to broad long-term mathematical success.
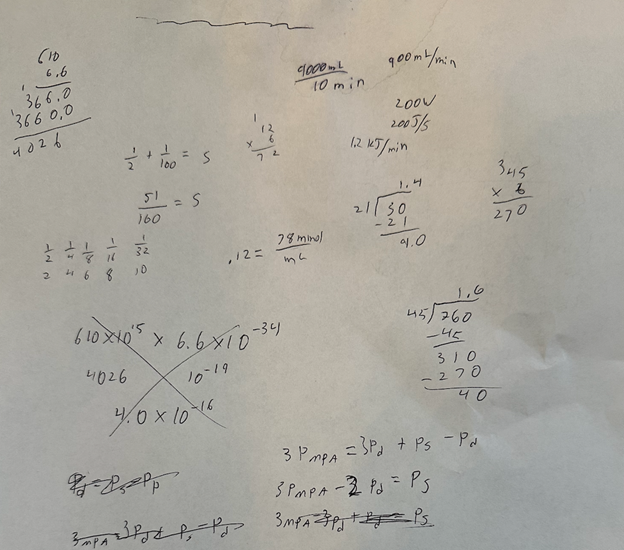
| The mistake that math educators often make is believing that to get high-level or advanced math performance, you must train on high-level or advanced math performance, but this is not how learning works generally. We are all built to learn component skills, the mastery of which is combined to become more complex composite skills or understandings. Think of a baby’s development in any area, language, for example. There are hundreds of component skills that must be mastered to result in a toddler’s rudimentary communication skills, for example, orienting and attending to another person, hearing the sounds coming from that person, attending to the immediate context of the sounds, attending to tone, producing some form of gestural or verbal response, experiencing feedback from the other person and environmental consequences for the communication (e.g., receiving a desired item). This series of skills is, in fact, an oversimplification of the actual process, but it hopefully makes the point that we can think of any ultimate performance goal (like communication) involving the mastery of dozens and even hundreds of component skills or behaviors. When humans attain mastery on component skills, composite skills often emerge without additional training when given the right opportunity (i.e., generalization) or require much less instructional opportunity to reach mastery. Thus, efficiency in instruction is gained by investing in the actual mastery of required component skills. |
I posted a comment in social media about how the use of calculators in math instruction can actually undermine math mastery and close doors to future educational and vocational paths in life, producing real economic constraints on a child’s future. This post got a lot of attention, including from well-meaning adults who believed that because physicians use tools like calculators to solve problems, then calculators should be the preferred format in education. What these well-meaning adults underplay is the science of how humans learn. Novice learners are not expert performers. Expert performers must have been at some point novice learners who experienced a sufficient dose of instruction (which is substantial) to gain expertise in a subject matter. Expert performers, when learning, are often generalizing. This can give the appearance that the learning is better and more efficient when tools like calculators or AI are used, but what is not seen in that process is the deep, foundational understanding being used to evaluate the most efficient way to arrive at a useful answer given the resource and context constraints on the particular problem to be solved. In a seminal paper in math education Star (2005) made exactly this point: that procedural skill development is not by definition shallow or rote but rather a necessary mechanism to help students develop the type of flexible problem-solving that we all aspire to build for our students. |

The reason mastery of foundation skills is necessary to enable flexible, efficient, and generative or creative problem-solving has to do with the science of learning. Learning is the most predictable outcome of highly effective instruction, and when learning is not happening, effective instruction has not occurred by definition. In behavioral psychology, there is a saying that “the learner is never wrong” (paraphrased from Keller, 1968) and what this statement conveys is that all learning can be defined as specific behaviors on the part of the learner that are susceptible to the environmental contingencies arranged by the teacher (e.g., task difficulty, task scope, task discriminability, opportunities to respond, corrective feedback). The goal of teaching is to improve students’ skill performance in noticeable, incremental ways until they reach levels of performance that will be useful to them in future learning.
Behavioral psychology and specifically, curriculum-based measurement (CBM), gave us the metrics (e.g., words read correctly per minute, digits correct per two minutes) to model academic learning in real time and enabled formative assessment. Formative assessment involves collecting sensitive information about the learning that is or is not happening in real time, providing feedback to the teacher so the teacher can change instructional variables to improve learning gains. Most systems embrace and routinely conduct universal screening and progress monitoring. But most systems struggle to use those data formatively. In other words, teachers have difficulty using progress monitoring data to know which instructional variables to adjust to promote learning for students. The Instructional Hierarchy (Haring & Eaton, 1978) is the framework that teachers need to help them teach more effectively in response to the student learning that is happening or not happening in front of them. CBM gives us the methodology to know when learning is happening. The Instructional Hierarchy (IH) tells us what to change in our teaching to bring about better learning.
If performance is in the frustrational range, the student needs acquisition instruction. Acquisition instruction emphasizes helping the student correctly respond and understand how and why that given response is correct and another response is not. This process is called stimulus discrimination in the behavioral literature, and specific instructional actions will assist with discrimination while others will be unhelpful or even counterproductive. Effective acquisition tactics include modeling correct responding with step-by-step explanations, checking for student accuracy at each step, providing immediate corrective feedback while students respond, and verifying prerequisite skill mastery.
When students do not correctly respond, the teacher might simplify or narrow the task presentation further and provide increasingly intensive prompts for correct responding (e.g., modeling, then guiding correct responding in real time with a gradual release or fading of support).
Once the student’s performance is in the instructional range (which means the performance is largely error-free), the student needs fluency building. Fluency building instruction makes giving the correct response easier for the student. Cognitive psychologists might call fluency automaticity. These are largely overlapping constructs with the defining feature being ease of responding. When the response can be given easily (without conscious effort according to cognitive psychology or rapidly and accurately according to behavioral psychology) the student has freed cognitive resources to think about what they are doing.
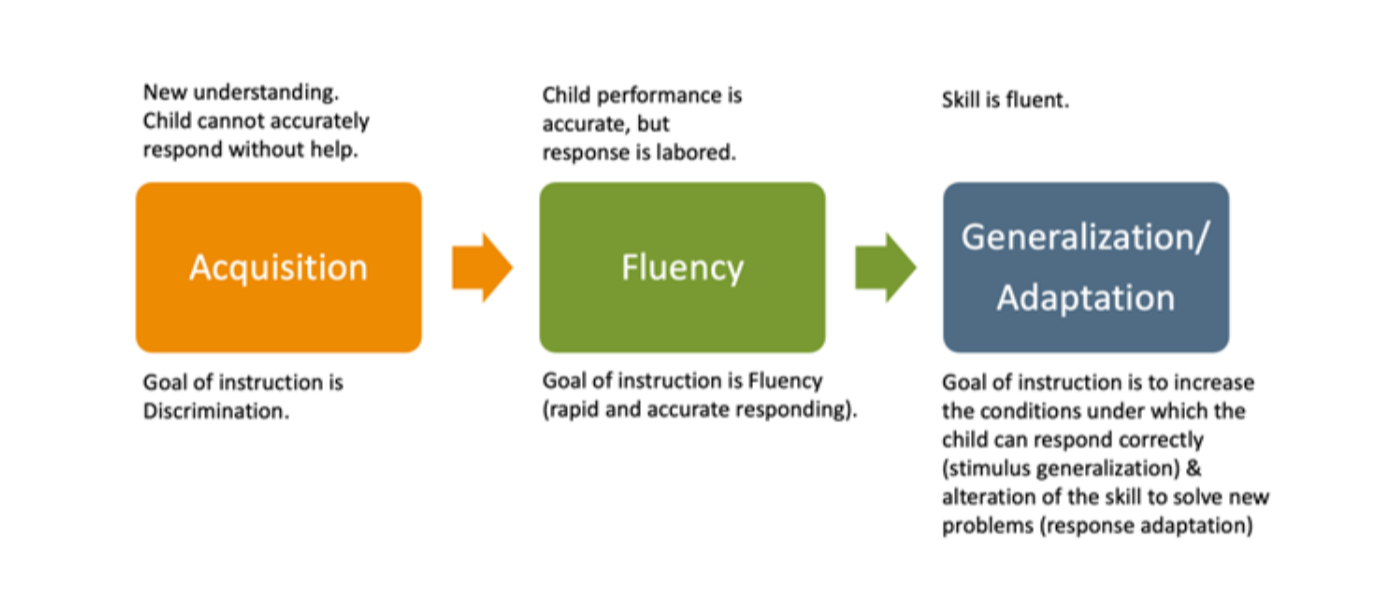
When students reach mastery, they are ready for generalization instruction. Students can generalize the learned skill — responding to previously untaught tasks and altering a learned response to solve more complex problems or to respond more efficiently. Generalization is where “free learning,” or learning without added instruction, can occur, which is very powerful in instruction. No teacher can effectively deliver generalization opportunities/instruction to students who have not acquired and reached mastery on the targeted skills. Thus, many teachers, leave such “free learning” on the table by moving on to new skills before current skills have been brought to mastery. The other problem that occurs in many classrooms is teachers attempt to use generalization instruction during the wrong stages of learning (i.e., when new skills are being introduced and students really need acquisition). Burns et al. 2010 famously illustrated this instructional mismatch calling it the “skill by treatment interaction.” When the right instruction is given according to the IH, performance improves. When the wrong instruction is given according to the IH, performance worsens, as shown below.
The Instructional Hierarchy is a foundational idea in academic skill intervention. Recently, Dr. VanDerHeyden recorded a session detailing the history of the Instructional Hierarchy and why it should be front and center in all models of academic instruction. This one-hour session can be found here. A timeline of the Instructional Hierarchy is shown below along with a list of key references for additional reading.
The Instructional Heirarchy

So to close the loop on our opening topic, calculators and such tools can be helpful when they are used by proficient learners to enable more complex problem-solving (e.g., multiple-step solutions on applied performance tasks). However, they are harmful to a student’s long-term mathematical proficiency when they are provided for students to use because teachers believe the students cannot solve the component skill computations without them. The intention and aspiration of the teacher are fantastic because the teacher probably believes that providing the calculator will allow the child to “access more challenging content.” But ultimately, a student is not able to access more challenging content or have more success solving more complex math because the student is lacking the building-block skills that open the door to flexible problem-solving. Only students who are proficient with computational and procedural skills can have appropriate expectations of operational effects on quantity at each step of a problem, to check whether their solution is tracking in the right direction step by step, to identify or think about a more efficient way to get to the correct answer, or solve the problem differently to double-check their final answer. Only proficient problem solvers can adapt (aka generalize) their responding to use the procedures that provide the level of precision that is needed to answer the question in the context in which it is being asked. Ultimately people who are proficient in math display this kind of fluid flexibility (aka fluency) in real time. When a child is not proficient in the fundamentals, the calculator may help them complete one computational step, but it will not help them construct the problem steps, track whether the solution is moving in the right direction given the problem details, and adjust their construction of the problem-solving steps for maximal ease and the precision they need in their answer.
References
Burns, M. K., Codding, R. S., Boice, C. H., & Lukito, G. (2010). Meta-analysis of acquisition and fluency math interventions with instructional and frustration level skills: Evidence for a skill by treatment interaction. School Psychology Review, 39(1), 69–83. https://doi.org/10.1080/02796015.2010.12087791
Haring, N. G., & Eaton, M. D. (1978). Systematic instructional procedures: An instructional
hierarchy. In N. G. Haring, T. C. Lovitt, M. D. Eaton, & C. L. Hansen (Eds.), The Fourth R: Research in the Classroom (pp. 23–40). Merrill.
Keller, F. S. (1968). "Good-bye, teacher...". Journal of Applied Behavior Analysis, 1 (1), 79–89. https:/doi.org/10.1901/jaba.1968.1-79
Star, J. R. (2005). Reconceptualizing procedural knowledge. Journal for Research in Mathematics Education, 36, 404-411. https://psycnet.apa.org/record/2005-13920-002
Additional References Specific to the Instructional Hierarchy
Burns, M. K. (2007). Reading at the instructional level with children identified as learning disabled: Potential implications for response-to-intervention. School Psychology Review, 22, 297-313.
Burns, M. K., Codding, R. S., Boice, C. H., & Lukito, G. (2010). Meta-analysis of acquisition and fluency math interventions with instructional and frustration level skills: Evidence for a skill by treatment interaction. School Psychology Review, 39, 69–83. https://doi.org/10.1080/02796015.2010.12087791
Burns, M. K., & Parker, D. C. (2014). Curriculum-based assessment for instructional design: Using data to individualize instruction. New York: Guilford.
Burns, M. K., VanDerHeyden, A. M., & Jiban, C. (2006). Assessing the instructional level for mathematics: A comparison of methods. School Psychology Review, 35, 401-418. https://doi.org/10.1080/02796015.2006.12087975
Burns, M. K., Riley-Tilman, T. C., & VanDerHeyden, A. M. (2012). RTI Applications, Volume 1. Academic and Behavioral Interventions. New York: Guilford. (226 pp.)
Codding, R. S., Shiyko, M., Russo, M., Birch, S., Fanning, E., & Jaspen, D. (2007). Comparing mathematics interventions: Does fluency predict intervention effectiveness? Journal of School Psychology, 45, 603-617.
Daly, E. J., Martens, B. K., Hamler, K., Dool, E. J., & Eckert, T. L. (1999). A brief experimental analysis for identifying instructional components needed to improve oral reading fluency. Journal of Applied Behavior Analysis, 32, 83–94.
Daly, E. J., Martens, B. K., Kilmer, A., & Massie, D. (1996). The effects of instructional match and content overlap on generalized reading performance. Journal of Applied Behavior Analysis, 29, 507–518.
Daly, E. J. III, Witt, J. C., Martens, B. K., & Dool, E. J. (1997). A model for conducting a functional analysis of academic performance problems. School Psychology Review, 26, 554-574.
Deno, S. L. (1985). Curriculum-based measurement: the emerging alternative. Exceptional Children, 52, 219-232.
Deno, S. L., & Mirkin, P. K. (1977). Data-based program modification: A manual. Council for Exceptional Children.
Eckert, T.L., Ardoin, S.P., Daly, E.J., III and Martens, B.K. (2002). Improving oral reading fluency: A brief experimental analysis of combining an antecedent intervention with consequences. Journal of Applied Behavior Analysis, 35, 271-281. https://doi.org/10.1901/jaba.2002.35-271
Gickling, E. E., & Armstrong, D. L. (1978). Levels of instructional difficulty as related to on-task behavior, task completion, and comprehension. Journal of Learning Disabilities, 11, 559–566.
Haring, N. G., & Eaton, M. D. (1978). Systematic instructional procedures: An instructional hierarchy. In N. G. Haring, T. C. Lovitt, M. D. Eaton, & C. L. Hansen (Eds.), The fourth R: Research in the classroom (pp. 23-40). Columbus, OH: Merrill.
Haughton, E. C. (1971). Aims- growing and sharing. In J. B. Jordan & S. Robbins (Eds.) Let’s try doing something else kind of thing: Behavioral principles and the exceptional child. Arlington, VA: Council for Exceptional Children.
Haughton, E. C. (1980). Practicing practices: Learning by activity. Journal of Precision Teaching, 1, 3-20.
Lentz, F. E., & Shapiro, E. S. (1986). Functional assessment of the academic environment. School Psychology Review, 15 (3), 346–357.
Maki, K. E., Zaslofsky, A. F., Knight, S., Ebbesmeyer, A. M., & Chelmo-Boatman, A. (2020). Intervening with multiplication fact difficulties: Examining the utility of the instructional hierarchy to target interventions. Journal of Behavioral Education, 30 (1), 1-25
McComas, J. J., Wacker, D. P., Cooper, L. J., Asmus, J. M., Richman, D., & Stoner, B. (1996). Brief experimental analysis of stimulus prompts for accurate responding on academic tasks in an outpatient clinic. Journal of Applied Behavior Analysis, 29 (3), 397-401.
Noell, G. H., Gansle, K. A., Witt, J. C., Whitmarsh, E. L., Freeland, J. T., LaFleur, L. H., Gilbertson, D. N., & Northup, J. (1998). Effects of contingent reward and instruction on oral reading performance at differing levels of passage difficulty. Journal of Applied Behavior Analysis, 31, 659–663.
Shapiro, E. S., & Lentz, F. E. (1985). Assessing Academic Behavior: A Behavioral Approach. School Psychology Review, 14 (3), 325–338. https://doi.org/10.1080/02796015.1985.12085178
Skinner, B. F. (1953). Some contributions of an experimental analysis of behavior to psychology as a whole. American Psychologist, 8, 69-78.
Starlin, C. M. (1971). Evaluating progress towards reading proficiency. In B. Bateman (Ed.), Learning Disorders, Volume IV. Pp. 390-465. Seattle, WA: Special Child Publications.
Starlin, C. M. (1982). Iowa Monograph: On Reading and Writing. State of Iowa, Department of Public Instruction. Des Moines, Iowa.
Starlin, C. & Starlin, A. (1974). Guides for continuous decision making. Bemidji, MN: Unique Curriculums Unlimited.
VanDerHeyden, A. M., Solomon, B. G. (2023). Valid outcomes for screening and progress monitoring: Fluency is superior to accuracy in curriculum-based measurement. School Psychology, 38 (3), 160-172. doi: 10.1037/spq0000528. PMID: 37184958.
White, O. R. (1986). Precision Teaching — Precision Learning. Exceptional Children, 52, 522-534.
